This is the transformation which is needed to convert a reading x'
in the K' system of coordinates to an x value in the K system, if K' moves
with a speed of v relative to the K system. According to classical Galileian / Newtonian
mechanics: x' = x - vt.
We are considering motion only along the x axis. y' and z'
remain the same as y and z, respectively.
A light signal along the positive x axis ( to the right )
of frame K is transformed according to the
equation x = ct, or x - ct = 0
(1)
Relative to K' the transformation is x' - ct' = 0 (2)
Space-time points ( called events ) which satisfy (1) must also satisfy (2).
i.e.
![]() where l
is a constant
(3)
where l
is a constant
(3)
In the negative direction ![]() where m is a constant
(4)
where m is a constant
(4)
Add (4) to (3)
![]()
![]()
![]()
i.e.
![]() (5 i)
(5 i)
where
and
.
Equation (3) ![]()
Equation (4) ![]()
Subtract (4) from (3) ![]()
So
that ![]()
i.e.
![]()
..So
that ![]() (5 ii)
(5 ii)
The problem now is to find the values of a and b.
For the origin of K', x' = 0
x' = ax - bct. ( Equation (5 i) ),
becomes ax - bct = 0.
![]() (6)
(6)
and
![]() or
or ![]() , and
, and ![]() .
.
v is the relative velocity of the two systems of co-ordinates.
The Principle of Relativity states: Relative to K the length of a unit measuring rod at rest to K', must be exactly the same as the length of the rod relative to K' of a unit measuring rod at rest to K.
Insert a particular value of t ( time of K ), e.g. t = 0,
Then (5 i) becomes x' = ax - bc(0),
So that x' = ax
If x' increases by 1 unit ( infinitesimally small ) ax = 1 so that ![]() (7)
(7)
Relative to K' where t' = 0 , eliminating t from equations (5 i) and (5 ii)
we get: bct = ax - x' and act = ct' + bx .
Thus ![]() and
and ![]() so that
so that ![]() .
.
![]() so that…..
so that…..![]() .
.
But ![]() and
and ![]() from (6)
from (6) ![]()
![]()
ie
![]()
so
that 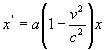 .
.
Thus points on the x-axis separated by distance 1 relative to K will be represented by the distance
x' = a ( 1 - v2 / c2 )1 and this must be equal to ![]() ( from (7)
)
( from (7)
)
![]() . Therefore
. Therefore ![]() (8)
(8)
Equations (6) and (8)
determine the values of a and b . Insert these values of
a and b in equation (5 i) :
![]()
![]()
![]()
![]()
The
Lorentz transformation for events on the x-axis.
The time t' can be derived from: ![]()
It equals the classical transformation divided by ![]()