or
\
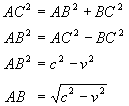
the Egyptian priests
knew that a triangle
with sides 3, 4 and
5, had a right angle
opposite the side of
length 5. ]
Part II
Now let us take the case of a moving medium, a river of width l and flowing at a steady speed v. We have two contestants, Alf and Ben, each with an identical motorboat and with identical throttle settings so that their speeds in still water are identical. Alf has to sail across the river from A to B and back. Ben has to sail downstream a distance l equal to the width of the river, and then back against the stream. On the downtrip over a distance l he is therefore assisted by the speed v of the stream, while on the uptrip he is retarded by the water flowing at a speed of v. Alf, going across the river and back again is not accelerated or retarded by the flowing water.
Who will win, or will it be a tie? Let's vote.
Tie…. Alf wins…. Ben wins….
( Picture to be loaded )
Alf must steer his boat in the direction AC so as to land at B. His speed is c, but his effective speed is indicated by length AB.
From Pythagoras' Theorem we know that:
| \ or \ |
 |
[ 4800 years ago, the Egyptian priests knew that a triangle with sides 3, 4 and 5, had a right angle opposite the side of length 5. ] |
Therefore Alf's time across and back
![]()
Ben's time down and up |
|
Alf's time Ben's time |
|
v2 / c2 is < 1 and 1 - v2
/ c2 is < 1 and when
v = c, we have ![]() . When v
is greater then c we have square root of 1 minus something greater than 1,
i.e. square root of something less than 1, which is impossible, proving than v
cannot be greater than c.
. When v
is greater then c we have square root of 1 minus something greater than 1,
i.e. square root of something less than 1, which is impossible, proving than v
cannot be greater than c.
Therefore Alf must win, because his time is less than Ben's time.
Now let us leave the slowly flowing river, and consider a rocket ship whose speed is v and whose diameter is d. Consider a ray of light ( speed c ) being sent across the rocket
( Picture to be loaded )
from mirror A to mirror B where it is reflected back to mirror A. This will happen as long as the ship is stationary. But when the ship moves at speed v, the mirror B will have reached point C when the ray of light reaches it.
Let the distance AC be indicated by x. Let AD ( = v ) be indicated by y. y ¸ x is called the time distortion factor in a spacial sense. In terms of velocity, the time distortion factor is given by v ¸ c, as is clear from the diagram.
By Pythagoras:
Thus |
\
\
\ \ |
|
This is the time distortion factor which tells us how much further the light ray must travel when the spaceship is moving compared to when it is stationary.
A graph of x/d against v/c shows that x/d increases exponentially for large values of v/c so that the values of x/d read from the graph, become inaccurate. But if we plot the inverse d/x against v/c, we obtain a graph from which all values of d/x can be accurately read off, for given values of v/c.
( Picture to be loaded )
ADDITION OF VELOCITIES
If Alf moves off from the Earth at velocity u and Ben moves off from Earth at velocity v, relative to Alf, what is Ben's velocity relative to Earth?
In other words, what is the sum w of Alf's and Ben's velocities? According to classical mechanics, we say w = u + v. But if u = 0.5c and v = 0.6c, say, then w = 0.5c + 0.6c - 1.1c, which is impossible because no velocity can be greater than the velocity of light c.
The product of the time distortions for Alf and Ben is xy and = w.
Thus
so that |
\
\ \ |
|
w cannot exceed c because:
![]()
subtracted from 1 is < 1.
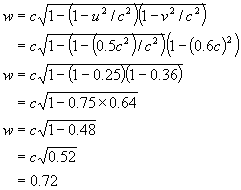
and not 1.1c.
A rigid measuring rod which moves at speed v will
contract so that its length at rest, l 0, becomes ![]() .
.
The mass of the body which moves at speed v will increase
so that its mass at rest m0 becomes ![]() .
.
At 0.99c, mass increases 7 times.
Time slows down so that
![]() .
.
For ordinary speeds v2 / c2 is infinitesimally small and 1 - v2 / c2 is practically equal to 1 - 0 and thus equal to 1. But when v becomes an appreciable fraction of c, the effect becomes noticeable.
Jets of Hydrogen are being ejected from the pulsar SS 433 at speeds of 80,000 km per second. These jets undergo precession and as they change over from approaching the Earth to receding from the Earth, there is still a residual velocity of 12,000km per sec. This is exactly 4% of the speed of light and is equal to the time dilation which takes place when the gasses are moving at 80,oookm per second or 26% of the speed of light. This is a beautiful confirmation of Einstein's theory of Special Relativity.
…..…..to be continued