ECLIPSING BINARIES. Stars that revolve around their mutual centre of gravity, their baricentre, will eclipse each other if the plane of their orbits lies in, or nearly in, the line of sight from the Earth. During their revolutions around each other they will eclipse and transit each other. This causes their total brightness to vary and thus they are classed among variable stars although the stars may not undergo any intrinsic variations. When these stars are to the left and right of each other, they are at their brightest and when they are in line with the line of sight from the Earth, they are at their dimmest.
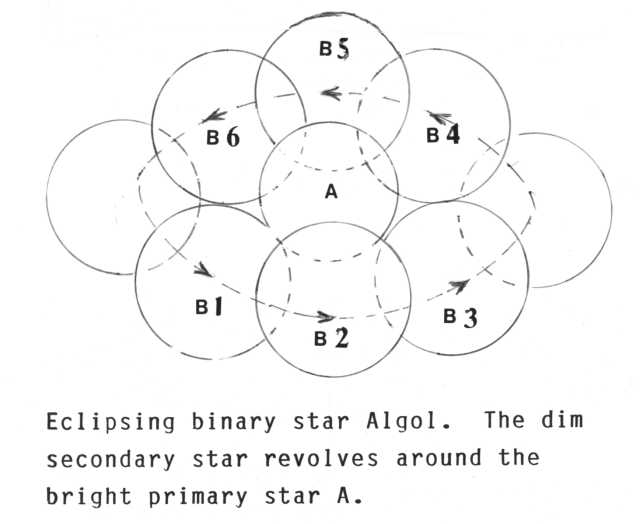
The first star of this sort to be discovered, was ALGOL (Ra's al Ghoel) or Beta Persei. Its variability was known in the days of the Babylonians and because it was the only star known to vary in brightness, having a period of 2 7/8 days (2,86731 days) it was called the Demon star. Its brightness varies from magnitude 2,12 down to magnitude 3,40. The eclipse of the brighter star by the dimmer star lasts about 10 hours. This is the lapse of time for star B to move from B1 to B3 on the Graph of variability. The deaf and dumb John Goodricke who lived to the ripe old age of 22 years, was the first to explain the variability (in 1782) to be due to the two stars of a double star, revolving around each other. When the dimmer star comes to the point B1 it just begins to eclipse the brighter star A. The fact that the light curve is curved downwards at point B1 is due to limb-darkening (just like the Sun). As the star B moves past in front of star A it cuts off more and more of the light from A and there is a steady decrease in brightness, the magnitude of the pair dimming from 2,12 down to 3,40 when the B-star is at point B2, its primary minimum. At B2 the brightness suddenly increases. This sudden increase in brightness shows that the eclipse is only partial or if it is total the two stars must be equal in size so that there is only one moment of minimum brightness. In the case of a total eclipse a measurable time will elapse while the dimmer star is transiting the brighter so that there will be a flattening in the graph.
At B3 when the dim star just stops eclipsing the bright star there is a curve in the light curve due to limb darkening.
As star B moves away from the primary star a slight increase in brightness takes place because of light from the primary being reflected from the surface of the dimmer star. Then a dimming of the total light takes place when star B moves in behind the brighter star A. The fact that there is now a flattening of the curve shows that the dimmer star is larger than the brighter because a measurable time elapses while the area of the light of B is cut off by A at B5.
Then limb darkening has its effect again before a slight dimming takes place as star B moves away from star A. The whole process then begins again from point B7 onwards.
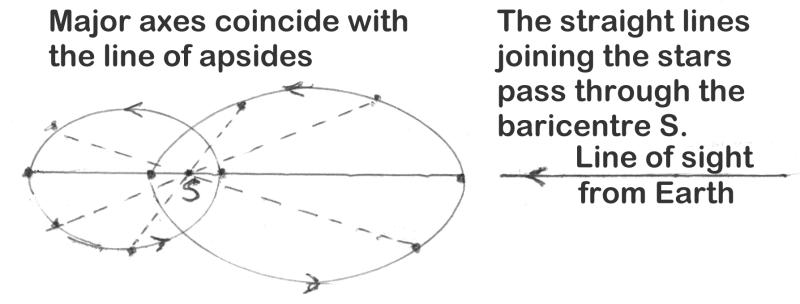
If the secondary minimum is exactly half-way between the two primary minima, it shows that the orbits of the stars are circles or the line of apsides, in which the major axes lie, is in the line of sight from the Earth.

If the secondary minimum is not exactly in the middle between the two primary minima, it shows that the orbits are ellipses. The greater the removal of the secondary minimum from the middle the greater the eccentricity of the ellipses. So the eccentricity of the orbits can be calculated from the position of the secondary minimum. In the case of Algol the eccentricity of the two orbits works out at 0,033 (nearer to circles than the orbits of six of the Sun's planets).
What else can one glean from the orbits of eclipsing binaries?
1. If the minima are rounded off, it shows that the atmospheres of the two stars are in contact with each other, such as in the case of Beta Lyrae.
2. By measuring the period of variability, the oeriod of revolution of the two stars is obtained. By applying Kepler's Third Law:
, the masses of the two stars and their separations from the baricentre can be calculated.
In the case of Algol the average distance of the bright star from the baricentre is 2,57 million km and that of the dimmer secondary 9 million km. Their masse's : are therefore in the proportion of 9 to 2,57 or 3,5 to 1 solar masses.
3. If both the primary and secondary minima are flattened, such as in U Sagittae, the diameters of the stars can be calculated by monitoring the moments of 1st, 2nd, 3rd and 4th contact. Then the absolute magnitudes and the separate magnitudes can also be calculated
4. The line of apsides which is the major axis of the two ellipses rotates in a period of 32 years. This is due to the gravitational perturbation of a third star in the system. The mass of the third body can also be calculated. It works out to 1,3 solar mass and it has an absolute magnitude of 3,2.
ALGOL |
Star A |
Star B |
Star C |
Mass ( x Sun ) |
3,5 |
1,0 |
1,3 |
Diameter ( x Sun ) |
3,0 |
3,4 |
1,5 |
Absolute Magnitude |
-0,2 |
3,4 |
3,2 |
Luminosity ( x Sun ) |
100 |
3,6 |
4,4 |
Spectral Type |
B8 V |
K0 IV |
F2 V |
Star |
R.A |
Dec. |
Magn |
itude | Period |
Spectral |
Algol Type |
Max |
Min |
days |
type |
||
| Beta Per | 03 07,0 |
+40 56 |
2,12 |
3,40 |
2,86731 | B8V; K0 IV; A |
| Delta Ori | 05 32,0 |
-00 18 |
1,94 |
2,63 |
5,7324 | B0 III; O 9V * |
| V Pup | 07 58,0 |
-49 14 |
4,7 |
5,2 |
1,454 | B IVp; B3 IV |
| CV Vel | 09 00,5 |
-51 32 |
6,5 |
7,3 |
6,889 | B0 V; B2 V |
| V 505 Sgr | 19 52,9 |
-51 32 |
6,48 |
7,50 |
1,182 | A0 V; F8 IV |
Beta Lyrae |
Type | |||||
| Beta Lyr | 18 49,9 |
+33 32 |
3,34 |
4,30 |
12,935 | B7 Ve; A8p |
| Mu1 Sco | 16 51,9 |
-38 03 |
2,8 |
3,08 |
1,44027 | B1,5 V; B6,5V |
| U Her | 17 17,2 |
+33 06 |
4,6 |
5,3 |
2,157 | B1,5 Vp; B5 III |
| UW Cma | 07 18,2 |
-24 34 |
4,84 |
5,83 |
4,39341 | O7 Ia; O |
| GG Lup | 15 18,9 |
-40 47 |
5,4 |
6,0 |
2,164175 | B5; A6 |
W Ursae M |
ajoris type | |||||
| S Ant | 09 52,3 |
-28 38 |
6,4 |
6,92 |
0,648345 | A9 Vn |
| YY Eri | 04 12,2 |
-10 28 |
8,8 |
9,5 |
0,321495 | G5; G5 |
| V502 Oph | 16 41,4 |
+00 30 |
8,34 |
8,84 |
0,453393 | G2 V; F9 V |
Jan Eben van Zyl