Part 1
It may seem impossible to measure the diameter of a star because even in the largest telescopes the images of stars are mere points of light - they do not show discs as planets do.
This very difficult problem was solved by making use of the nature of light itself, when two light waves are in step or in phase so that the crests of one wave coincide with the crests of the other wave, the amplitude of the wave is increased; but when the crests of one wave coincide with the troughs of the other wave, the two waves will annihilate each other and there will be darkness. This phenomenon is known as INTERFERENCE.
When the spot of light formed by the image of a star on a photographic plate is viewed through a microscope, an Airy disc is seen. It consists of a bright spot in the centre surrounded by alternate rings of dark and light.
If a ray of light is split into two parallel beams and these are sent through two parallel narrow slits, the light going through the two slits undergoes interference and alternate light and dark strips are formed.
The distance that the ray travels which forms the first dark strip is exactly one half wavelength more than the distance to the central bright strip. Then the distance that the next ray travels to the second bright strip is again exactly one half wavelength longer and so on.
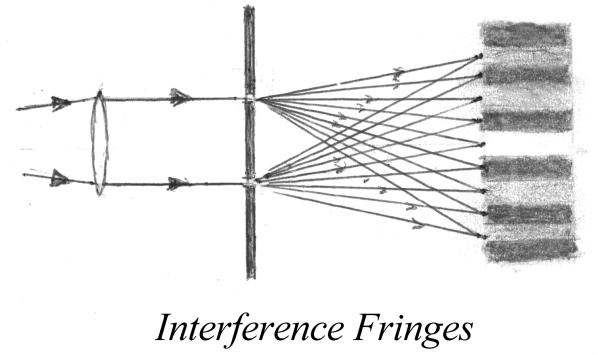
Let us isolate the first dark strip ( fringe ) in the following diagram.
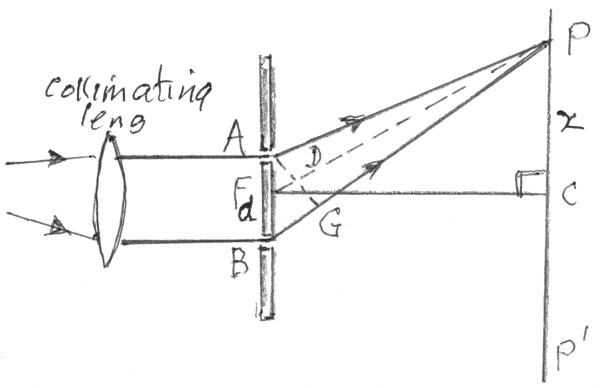
A and B represent the two very narrow slits, very close
together d apart.
Sunlight passes through the collimating lens so that the rays falling on A and B
are in parallel and in phase.
P C P' is a ground glass screen on which the light and dark fringes can be seen.
The point P is so situated that BP is one-half wavelength
longer than AP. A+P the two waves are thus out
of phase and cancel each other out thus forming a dark band or fringe. Beyond P
there will be another bright fringe followed by another dark fringe and so on. Similar
fringes will be formed between C and P'.
At C, which is equidistant from A and B, the crests of the two waves AC and BC will coincide and strengthen each other to form a bright fringe.
Since the distance AB ( = d ) is very small, arc AG with P as centre, can be considered a straight line. The arc AG thus forms right angles with both GP and AP because AP and GP are radii of the circle having P as the centre.
The two triangles BGA and PCF are similar, having two angles of the one equal to the corresponding angles of the other. Therefore the lengths of sides opposite equal angles are proportional.
i.e. CP = FP ( opposite angles
PFC and PCF )
BG AB ( opposite
angles BAG and BGA )
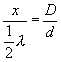or 
or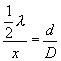 
.
Distance is known and distances x and D can be measured
so that the wavelength 
can be calculated
from 
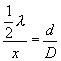so that 
.
For example, if D is 5 metres and d 1 millimetre i.e 10-3 metre,
the wavelength will be 
metres.
If the distance between fringes x is, say 1,5mm ( = 1.5 x 10-3
metre ), will come to
= 0,6 x 10-6
= 6000 x 10-10 metres
= 6000 Angstroms.
Alternatively, if the wavelength is known, the distance d between the
sources of the light rays can be calculated if x and D are measured.
The distance d could be the diameter of a star with points A and B on opposite sides of a diameter through the star ( = d )
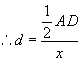
( to be followed in part II )
Jan Eben van Zyl