CANOPUS 02/06 - How did Kepler do it?

Kepler's analysis of the positions of Mars as measured by Tycho Brahe led him to formulate his first two laws in 1609.

The radius vector from the Sun to the planet sweeps out equal areas in equal periods of time.

We saw in parts I and II of this series of articles on Kepler, how he determined the distances of the planets from the Sun, relative to the Earth's average distance from the Sun, 1 astronomical unit. Kepler obtained the values given in the table:

Planet	Period of Revolution	Period in years = T	Average Dist. from Sun = R
Mercury	88 Days	0,241	0,387
Venus	225 Days	0,616	0,725
Earth	365.25 Days	1,000	1,000
Mars	687 Days	1,881	1,524
Jupiter	4333 Days	11,86	5,2
Saturn	10760 Days	29,46	9,54

Looking at the figures in the table, Kepler saw that the longer the period of revolution, the greater the average relative distance from the Sun. While Mercury's period is 0,241 years, that of Saturn is 29,46 years, i.e. 122.2 times greater. The relative distances of the two planets increased from 0,387 to 9,54 AU, i.e. 24,65 times. What relationship could there possibly be between 122,2 and 24,65? It seemed as if Nature was fickle. Nine years long Kepler battled with the figures and during that period of time he had to defend his 69 year old mother who had been charged with witchcraft! The case dragged on for three years.

By 1618 Kepler had succeeded in cracking the puzzle. He had found that there was a definite mathematical relationship between the SQUARES of the times of revolution and the CUBES of the average relative distances from the Sun.

Planet	T in years	T²	Dist. R in AU	R³	T²÷ R³
Mercury	0,241	0,058	0,387	0,058	1,000
Venus	0,616	0,379	0,725	0,381	0,995
Earth	1,000	1,000	1,000	1,000	1,000
Mars	1,881	3,538	1,524	3,539	1,000
Jupiter	11,86	140,6	5,200	140,6	1,000
Saturn	29,46	867,9	9,540	868,2	0,999

The table showed that T² ÷ R³ = Constant = 1,000, namely that the SQUARE of the period of revolution (in years) is proportional to the CUBE of the average relative distance in astronomical units. This relationship was also found to hold for Jupiter's four moons as well as for the planets, Uranus, Neptune and Pluto which were discovered later. This was Kepler's Third Law.

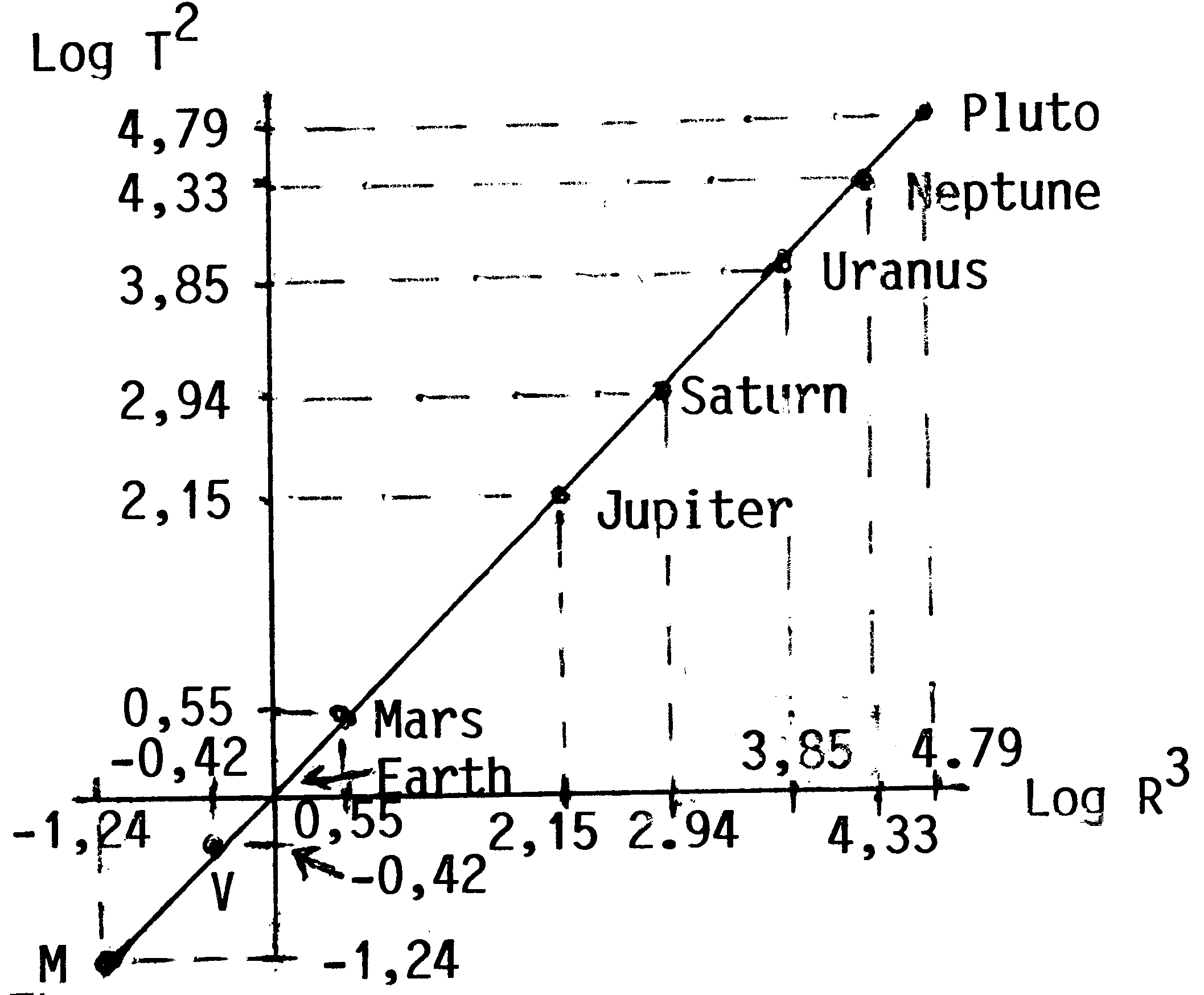
To represent Kepler's Third Law graphically, it is best to use the logs of the numbers. (The log of a number is the power to which 10 has to be raised to equal the number, e.g. the log of 100 is 2 because 100 = 10 raised to the power 2.)

The straight line shows the linear relationship between the squares of the times of revolution and the cubes of the average distances from the Sun.

Isaac Newton used Kepler's finding, that T² = R³ to derive the Law of Gravitation. Robert Hooke had suggested that circular motion necessitated a force towards the Centre. Newton found this force to be balanced by the centrifugal force in circular motion by F = m x R ÷ T², where F is the force of attraction of the Sun; m is the mass of the planet and T is the planet's time of revolution in years.

Substituting Kepler's value of R³ for T², Newton obtained the relation: F = m R ÷ R³, so that F = m ÷ R², i.e. the Sun's force of gravitation is proportional to the mass of the planet (m) and inversely proportional to the SQUARE OF THE DISTANCE, which is the Law of gravitation.

When double stars were discovered by William Herschel more than a century later, it was found that they obeyed Newton's Law of gravitation and also Kepler's Third Law.

By using Kepler's law: T² = R³, = Constant, it became possible to calculate the sum of the masses of the two stars of a binary system, simply by measuring the period of revolution of the two stars around their mutual Centre of gravity, their baricentre. After a double star has been observed for at least one complete revolution, the shape of the elliptical orbits can be derived, as well as the sizes of the two ellipses. This enables the ratio of the two stellar masses to be calculated. From this ratio and the sum of the masses, the individual masses are easily deduced. For example the sum of the masses of the two members of Alpha Centauri works out to be 1,96 solar masses. The ratio of the sizes of the two ellipses is 55 : 43, so that the individual masses work out to 1,1 and 0,86 solar masses. Being a G2 V star; Alpha Centauri-A of mass 1,1 solar mass is very similar to the Sun.